作为Data mining 的第一篇 先来讲讲频繁模式

频繁模式是推荐算法的基础

主要解决的是从一堆数据中挖掘出频繁的组合模式

举个简单的例子

可能买了Mac的人，过几天会去买贴膜
可能买考研英语书的人，过几天会去买考研数学书

如何在大量数据中找到可能相关的几个问题，称之为Frequent Pattern

频繁程度通过支持度、置信度两个参数来衡量

A->B support: 即模式A, B出现频率
A->B configure: 即模式A发生情况下B发生的概率

# Item Sets

Item Sets指的是假设不考虑数据之间的顺序

# Apriori

我们可以得出

• 如果一个集合是频繁集，那么它的所有子集都是频繁集
• 如果一个集合不是频繁集，那么它的所有超集都不会是频繁集

根据这一点，Agrawal & Srikant 在94年提出了著名的Apriori算法

主要思想就是从大小1开始遍历可能频繁集k
当满足V所有集合子集都在之前计算过的频繁集k中，且出现次数满足频繁要求
则V为k+1频繁集

伪代码:

Ck: Candidate itemset of size k
Lk : Frequent itemset of size k

L1 = {frequent items};
for (k = 1; Lk !=; k++) do begin
     Ck+1 = candidates generated from Lk;
    for each transaction t in database do
       increment the count of all candidates in Ck+1
    that are contained in t
    Lk+1  = candidates in Ck+1 with min_support
    end
return k Lk;

举个简单的例子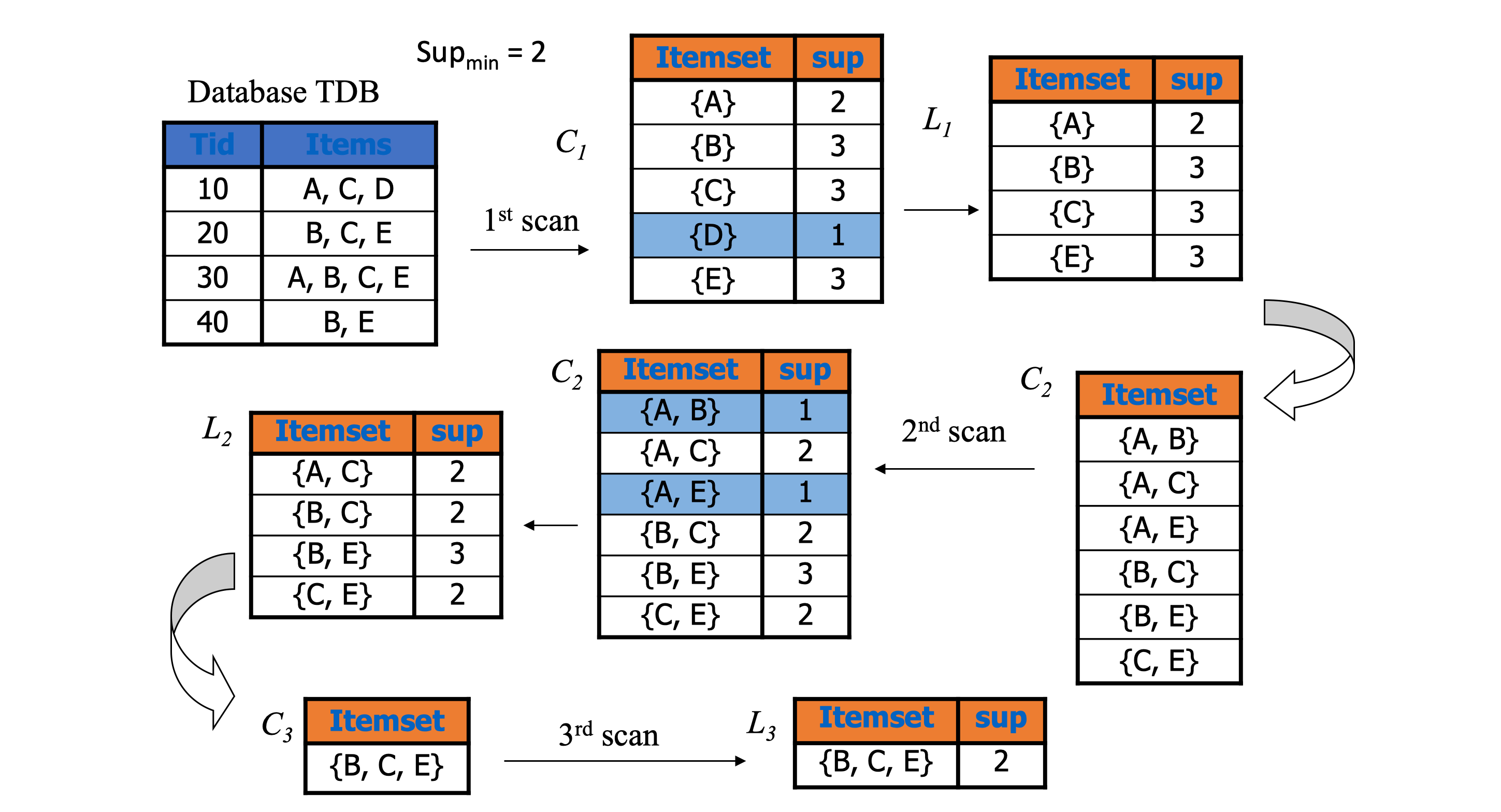

但Apriori也有一些缺点

1. 多次读取数据，复杂度高
2. n较大，可能的取值较多

Apriori也有一系列改进算法，比如说用hash存储可能的取值，做剪枝等等

# FP-tree

仔细想一下上述算法的实现过程

一层层扩展，从大小为1开始，到2，再到k，到k+1

是不是很像BFS

那么我们不免想是不是会有类似DFS的算法

Jiawei Han, Jian Pei 在2000年提出FP-tree算法

通过构造前缀树来实现类似深度搜索的算法

先把所有集合按字母出现频次逆序排列，筛选出现频次小于min_support值的项

然后找所有DB中所有满足当前前缀abc的项，DB|abc

依次遍历

算法通过前缀树Trie实现

举个简单的例子

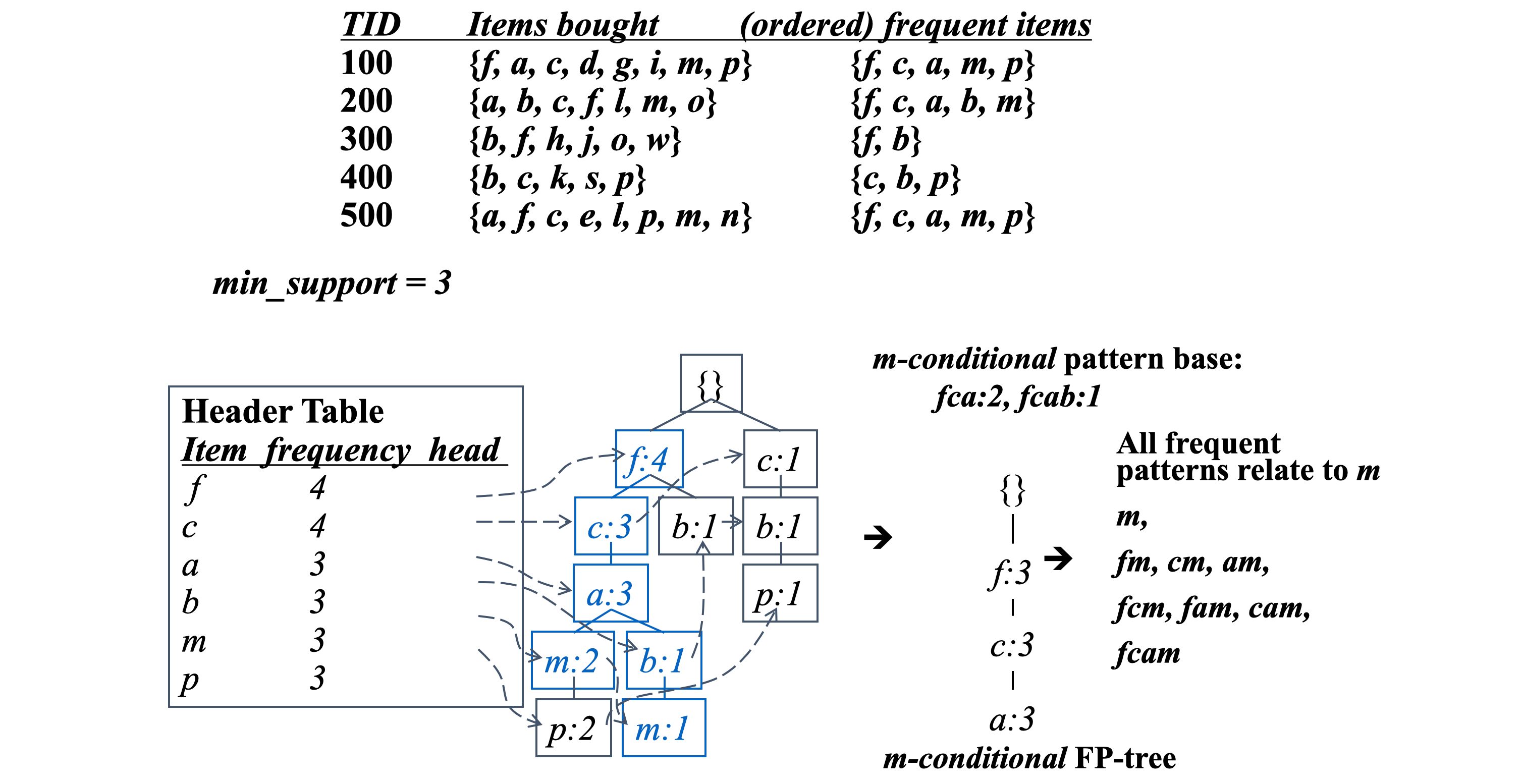
# Sequences

刚才说到的Item Sets中间的数据为无序的，但实际中，很多频繁集是在特定顺序下才成立的

Sequence主要研究的就是带有顺序的情况, 把每次操作的项放在集合Si中，集合S1, S2, ...,Sn组成序列集

同样求在最低支持度下所有的频繁集

# GSP

Join Phase在96年提出类似Apriori的算法GSP

和Apriori唯一的差别就是如何计算子集

现在GSP中的集合S为集合的集合

定义S的子集C满足

1. Ci为Si的非空子集, 当i∈[2, n-1]
2. Ci为Si的子集, 当i==1 | i==n

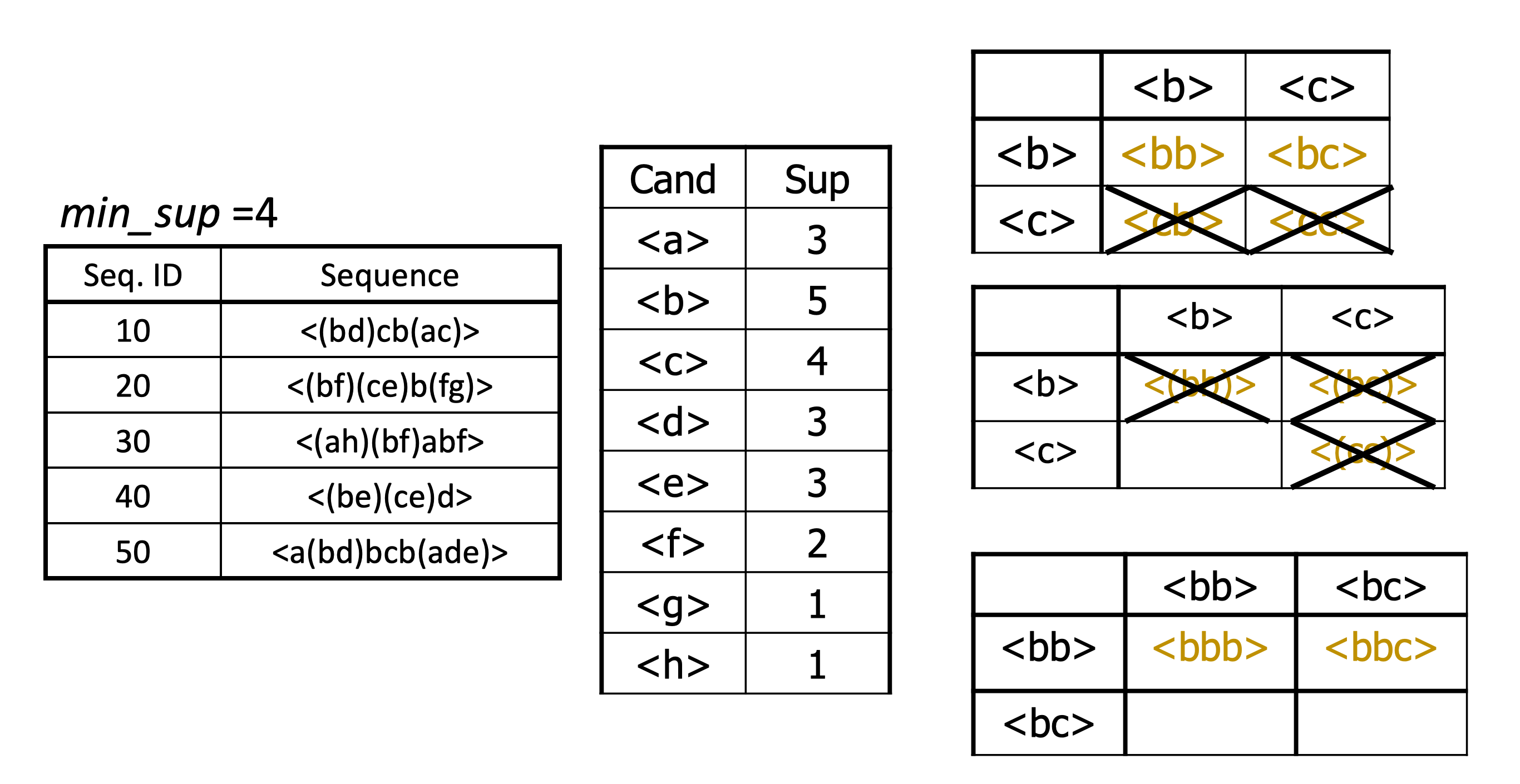
# PrefixSpan

PrefixSpan 全称为Prefix-Projected Pattern Growth

前缀投影就是后缀Suffix，那么什么是前缀和后缀呢

定义 <a(abc)(ac)d(cf)>的前缀、后缀为

PrefixSpan的思路就是

从a开始遍历所有满足min_support的前缀

然后对后缀检查是否满足min_support，若所有项都满足，则保留满足项

然后依次合并前缀项，递归遍历

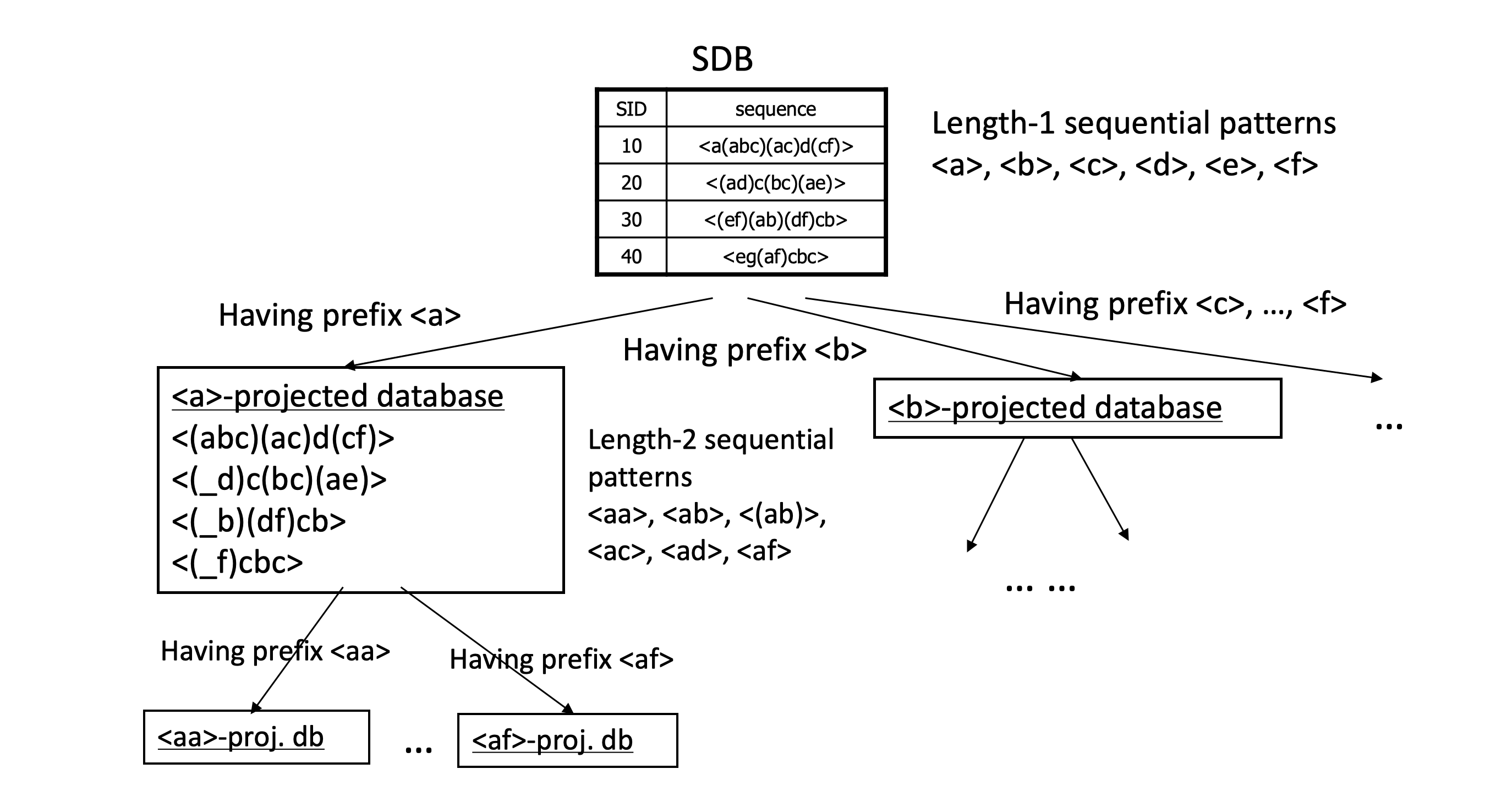
# Tree patterns

当前面的集合推广到数结构

解决的主要是类似于网站链接的场景

# 范围编码

思考这么一个问题

有一颗树 如何判断是否是节点A是不是节点B的祖先

一般一点的办法就是以A为root节点，向下遍历，如果遍历到B则说明A是B的祖先

但这样很显然当树的规模比较小的时候还可以，但一旦树结构复杂时，就会接近O(n), 尤其是需要多次查找时

有人就想出一个O(1)的算法

先 先序遍历 一次树，第一次遍历到该节点时记录时间为Tleft, 再次到节点记为Tright

用区间[Tleft, Tright]表示该树的祖孙关系

当A节点的区间为Ka，B节点的区间为Kb时

• 若Kb属于Ka，则A为B的祖先
• 若Kb∩Ka=∅，则A, B为广义兄弟

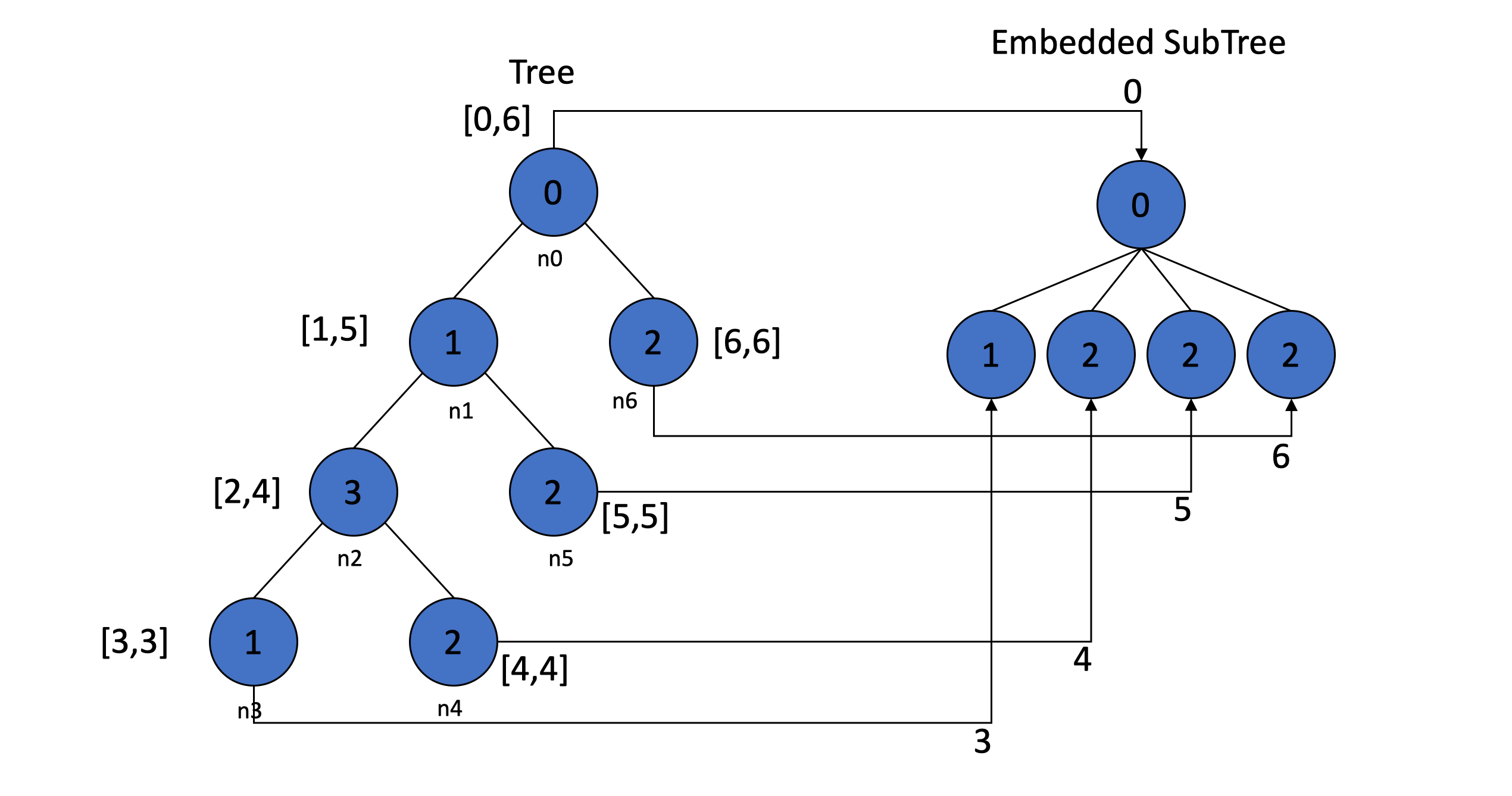
只要遍历一次建立区间索引之后，再次确认节点间的祖孙关系只需O(1)

# String Representation of Trees

利用string表示一棵二叉树

按先序遍历二叉树

• 如果第一次遍历到该节点则输出节点值
• 如果到达边界条件，跳出递归则输出-1

那么可以利用输出的节点值唯一的表示一棵二叉树

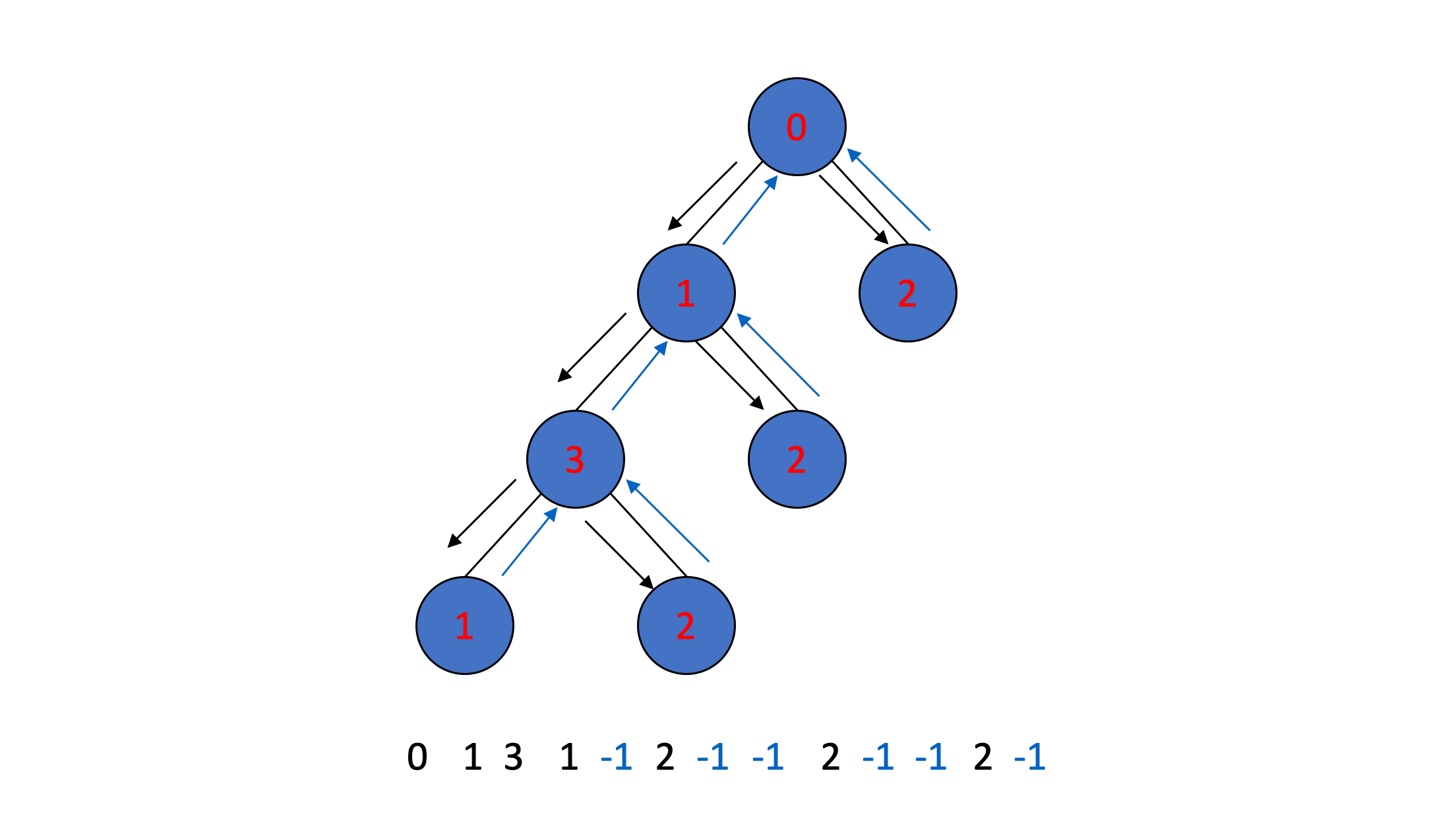
# Equivalence Classes

因为前面用String来表示一棵树

如果两棵树具有相同的前缀，我们就称这两棵树为Equivalence Classes

举个例子, 右侧的几棵树都有相同的前缀3 4 2 -1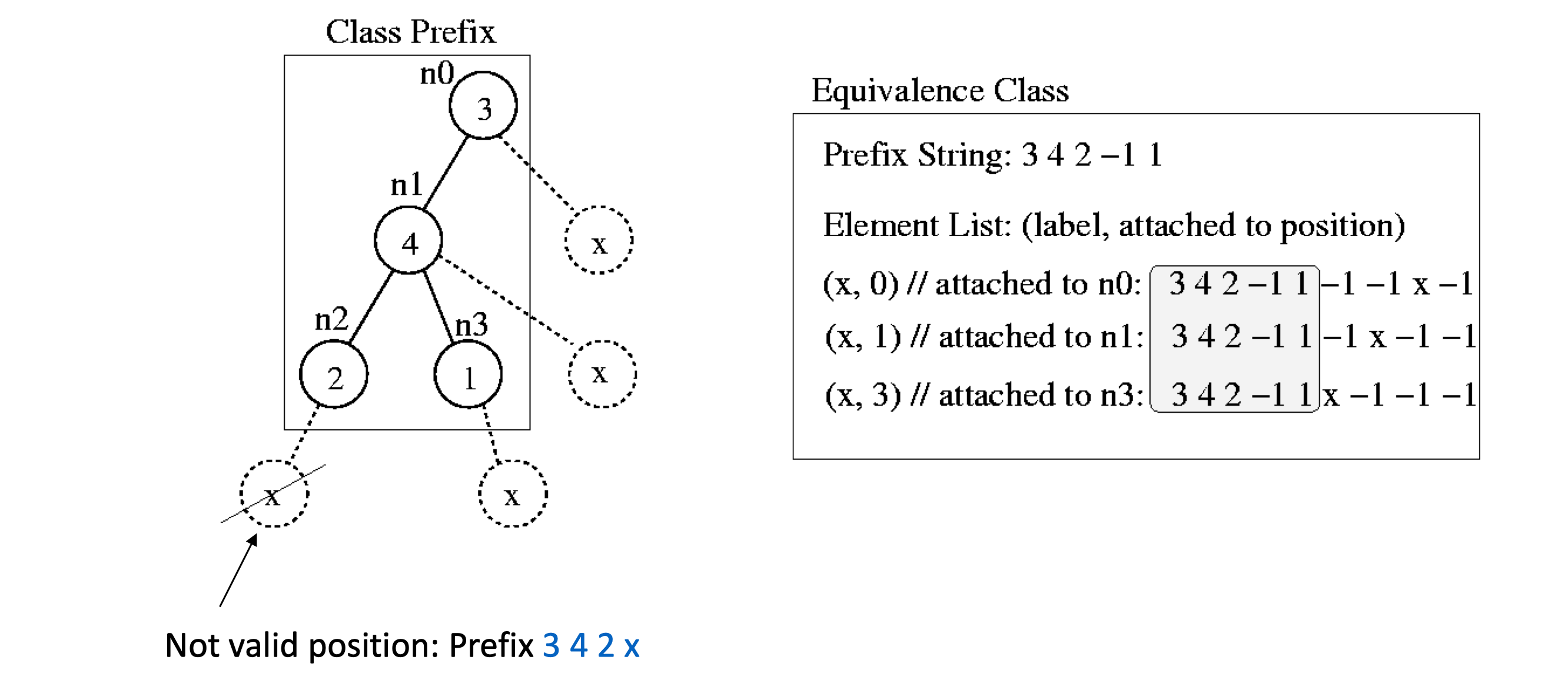

其中Element List(m, n)中m指的是插入值，n为父节点id

# TreeMiner

当我们用String来表示一个一棵树的时候，那么我们就把问题转化成Sequence Pattern

Mohammed Javeed Zaki在2002年提出TreeMiner算法

当父节点包含子节点，则链路可以加长

for each element (x, i) ∈ [P] do
    [Px] = ∅;
    for each element (y, j) ∈ [P] do
       R = {(x, i)⊗(y, j)};
       L(R) = {L(x) ∩⊗ L(y)};
       if for any R ∈ R, R is frequent then
          [Px] = [Px] ∪ {R};
    Enumerate-Frequent-Subtrees([Px]);

举个🌰

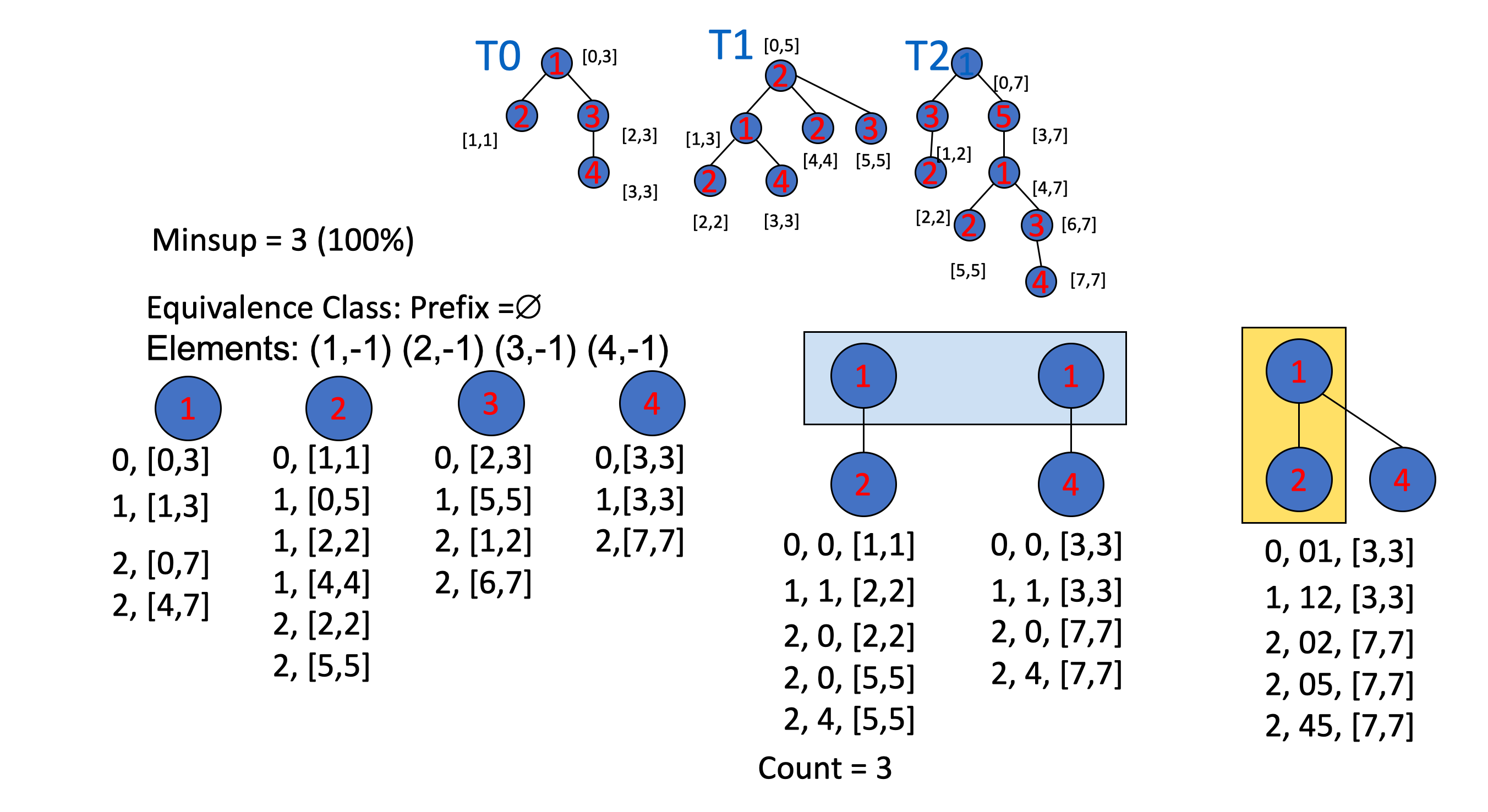
# PrefixTreeESpan

上面TreeMiner算法类似于Apriori，属于DFS类型的算法

于是很容易想到是否有类似于FP-tree，PrefixSpan属于BFS的算法

Lei Zou, Yansheng Lu等人在2006年提出PrefixTreeESpan算法

从结构上看，从一个节点开始，找所有满足该前缀的结构

如果该结构的个数满足min_support则进入下一步

对所有后缀结构首位进行分析，如果满足前缀-后缀首位的结构数大于min_support时，则进入下一部

直到没有可分析的结构 则该结构为频繁树

举个栗子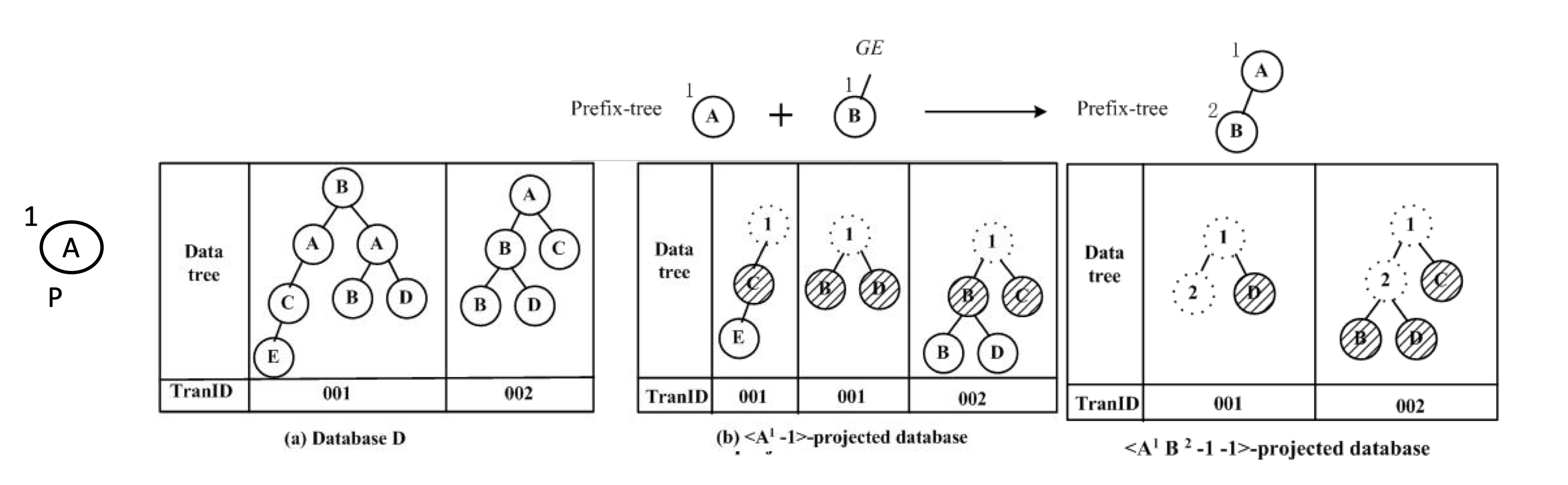

# Graph Pattern

如果我们把前面的树结构再进一步推广到图，那么我们要求的就是频繁子图

# AGM

AGM = Apriori-base graph Mining

1. S1  数据集中的单个频繁元素;
2. 调用AprioriGraph(D, min_sup, S1)
   Procedure AprioriGraph(D, min_sup, Sk)
 {   1.  初始化Sk+1
     2.   For each 频繁子图 gi ∈Sk
     3.        For each频繁子图 gj∈Sk
     4.             For each 通过合并gi和gj形成规模为(k+1)的图g
     5.                    If g是频繁的，并且g不属于 Sk+1
     6.                              把g插入Sk+1
     7.   IF  Sk+1不为空， then调用AprioriGraph(D, min_sup, Sk+1)
  }

Akihiro Inokuchi提出用邻接矩阵存储图数据，通过basket analysis得到图的频繁子图

通过定义编码方式把n×m的矩阵变成水平扩展的string

与Apriori算法类似，候选频繁子图的生成是根据子图的大小通过水平搜索来进行的

令Xk和Yk是两个大小为k的频繁图G(Xk)和G(Yk)的顶点排序的邻接矩阵

如果G(Xk)和G(Yk)除了第k行和第k列的元素之外具有相等的矩阵元素，则它们被连接以生成Zk+1

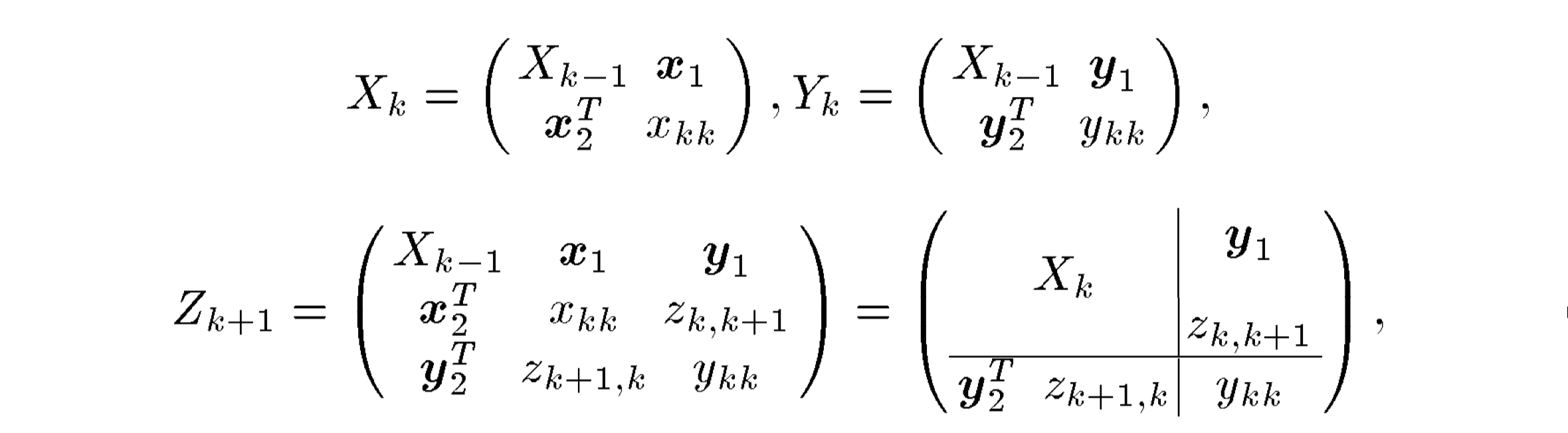
# FSG

Framework in FSG:
Step1.  Enumerating all frequent single- and double-edge subgraphs;
Step2.  Generating all candidate subgraphs whose size is greater than the previous ones by one edge.  (Ck)
Step3. Count the frequency for each of these candidates and prune infrequent subgraph patterns. (Fk)
Step4. | Fk |=0, STOP; otherwise k=k+1, and goto Step 2.

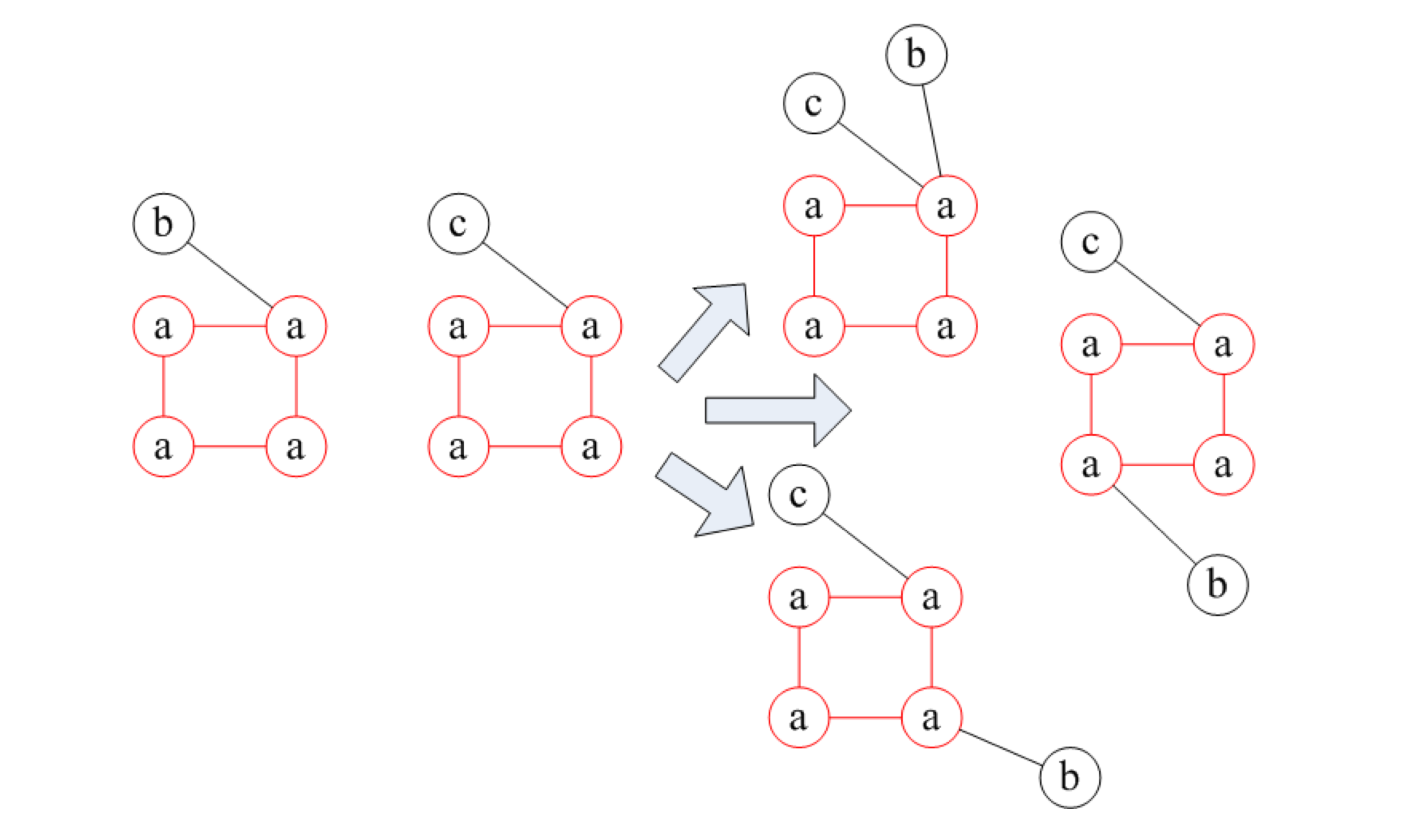
# gSpan

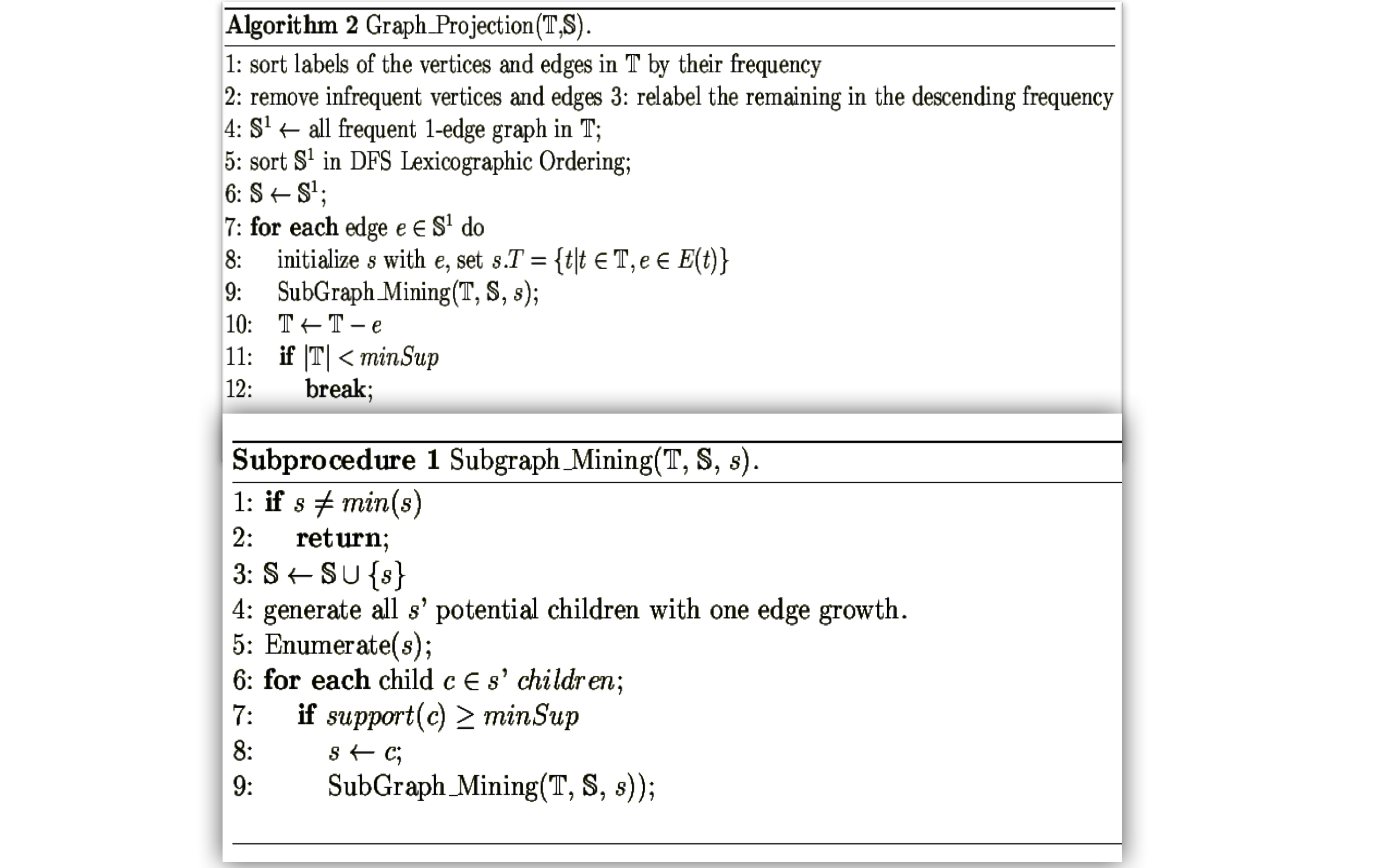
额 最后有点水了 等我消化消化 再来写

# 参考

1. Fast Algorithms for Mining Association Rules
2. Mining Frequent Patterns without Candidate Generation
3. Mining Sequential Patterns: Generalizations and Performance Improvements
4. PrefixSpan: Mining Sequential Patterns Efficiently by Prefix-Projected Pattern Growth
5. Efficiently Mining Frequent Trees in a Forest
6. PrefixTreeESpan: A Pattern Growth Algorithm for Mining Embedded Subtrees
7. An Apriori-based Algorithm for Mining Frequent Substructures from Graph Data
8. gSpan: Graph-Based Substructure Pattern Mining